#6 Công thức tính thể tích [KHÔNG THỂ BỎ QUA]

Thể tích là gì?

Thể tích của một hình hoặc là một vật có thể là dung tích chính là lượng không gian mà vật ấy chiếm, là giá trị mà hình đó chiếm bao nhiêu phần trong tổng không gian ba chiều. Bạn cũng có thể hiểu là thể tích của một hình là lượng nước cũng có thể là không khí hoặc lượng cát,… mà hình đó có thể chứa khi làm đầy bằng các vật phía trên. Theo như hệ đo lường của quốc tế thì đơn vị để đo khoảng cách là mét còn đơn vị để đo thể tích chính là mét khối, được ký hiệu là m³ (m3).

Đơn vị tính thể tích

Đơn vị độ dài nào cũng có đơn vị thể tích tương ứng, thể tích của khối lập phương sẽ có các cạnh với chiều dài nhất định. Ví như như là 1 cm3 là thể tích của khối lập phương có cạnh là 1cm.

Trong hệ đo lường SI thì đơn vị chuẩn của thế tích sẽ là m3. Hệ mét cũng bao gồm các đơn vị là lít (litre) được ký hiệu là L, nó như là một đơn vị của thể tích, trong đó có một lít là thể tích của khối lập phương là 1dm. Ta có thể hiểu như sau:

• 1 lít = 1 dm3 = 1000 cm3 = 0.001 m3 vậy 1m3 = 1000 lít.

Lượng chất lỏng nhỏ sẽ được đo bằng đơn vị là mililit (ml) tên tiếng anh là milliliter

• 1 ml = 0.001 lít = 1 centimet khối.

Một lượng lớn chất lỏng sẽ được đo bằng đơn vị là megalit tiếng anh viết là Megalitre

• 1 000 000 lít = 1000 mét khối = 1 mega lít (Ml).
• (Lưu ý rằng Megalitre được kí hiệu là Ml, không phải ký hiệu ml như milliliter).

Các công thức tính thể tích

Bạn đang muốn tính thể tính của cột nhà, bể bơi,… mà vẫn chưa tìm được công thức tính thể tích phù hợp hoặc chưa biết tính như thế nào? Hãy xem ngay các cách tính dưới đây nhé.

• Hình lập phương

Hình lập phương là hình khối ba chiều và có 6 mặt đều là hình vuông. Được hiểu là hình hộp có tất cả các cạnh bằng nhau. Ví dụ các loại hình lập phương mà các bạn thường thấy đó là viên xúc xắc có 6 mặt, viên đường nén hoặc là khối học chữ của trẻ con.

– Công thức tính thể tích của hình lập phương

Bởi các cạnh của hình lập phương đều bằng nhau nên thể tích cũng khá là đơn giản. Được tính như sau: V = s3.

=> Trong đó:

• V là thể tích
• Để tìm s3 thì ta nhân s với chính nó 3 lần.

– Cách tính chiều dài một cạnh của hình lập phương:

Tùy vào đề bài cho sẵn các giá trị hoặc là ta phải tự đo cạnh của hình bằng dụng cụ là thước. Vì các cạnh bằng nhau nên ta chỉ cần đo 1 cạnh bất kỳ. Nếu như bạn chưa chắc chắn hình bạn cần tính là hình lập phương thì bạn nên đo tất cả các cạnh.

• Hình hộp chữ nhật

Hình hộp chữ nhật còn được gọi là lăng kính chữ nhật, nó là hình khối ba chiều với 6 mặt giống nhau đều là hình chữ nhật. Hình hộp chữ nhật đơn giản là hình chữ nhật có 3 chiều hoặc là hình hộp. Hình lập phương là dạng hình đặc biệt của hình chữ nhật.

– Công thức tính thể tích của hình hộp chữ nhật

Công thức được tính như sau: V = I*w*h

=> Trong đó:

• V là thể tích
• I là chiều dài
• w là chiều rộng
• h là chiều cao

– Cách tìm chiều dài, rộng, cao của hình hộp chữ nhật

+ Chiều dài: là cạnh dài nhất của hình chữ nhật nằm song song với mặt phẳng đặt hình. Nếu như bạn không phân biệt được đâu là chiều dài đâu là chiều rộng và đâu là chiều cao thì bạn chỉ cần đo 3 kích thước khác nhau rồi nhân các giá trị đó lại với nhau.

+ Chiều rộng: là cạnh ngắn hơn của mặt song song với mặt phẳng đặt hình hộp. Bạn có thể sử dụng thước để đo, nhưng lưu ý là tất cả các phép đo cần chung một đơn vị.

+Chiều cao: là khoảng cách từ mặt phẳng đặt hình tới mặt trên của hình hộp. Bạn cũng có thể xác định giá trị bằng cách dùng thước đo để xác định các giá trị.

• Hình nón

Hình nón là khối không gian ba chiều có mặt đáy là hình tròn và nó chỉ có một đỉnh duy nhất. Bạn có thể hiểu là hình nón có đáy là hình tròn. Nếu như mà hình chiếu của đỉnh xuống mặt đáy của hình trùng với tâm của mặt đáy thì ta gọi đó là hình nón đều. nếu ngược lại thì ta sẽ gọi đó là hình chóp xiên.

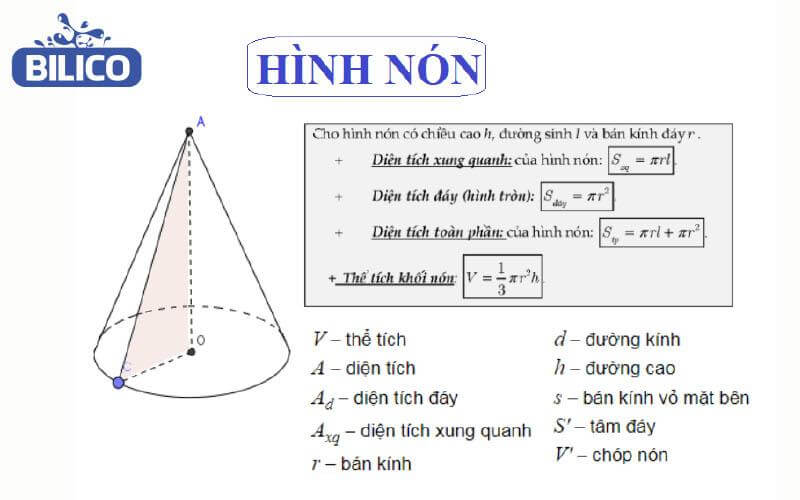
– Công thức tính thể tích của hình nón

Công thức được tính như sau: V = 1/3πr²h

=> Trong đó:

• r là bán kính của mặt đáy
• h là chiều cao của hình nón đó
• π là hằng số pi, làm tròn lấy giá trị là 3.14

Trong công thức đó thì πr² là diện tích của mặt đáy.

• Hình cầu

Hình cầu là vật thể của không gian tròn hoàn toàn với khoảng cách từ 1 điểm bất kỳ đến tâm của hình là không đổi. Có thể hiểu hình cầu chính là hình của quả bóng.

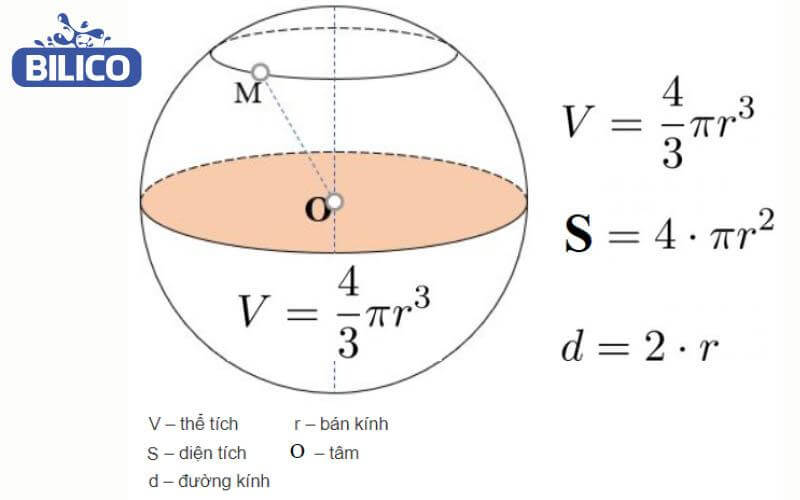
– Công thức tính thể tích của hình cầu

Được tính như sau: V = 4/3π³

=> Trong đó:

• r là bán kính hình cầu
• π là hằng số pi có giá trị là 3.14.

– Cách tìm bán kính của hình cầu

Nếu như mà đề bài không cho sẵn bán kính thì ta tìm bằng cách là chia đôi đường kính.

– Cách đo bán kính nếu chưa biết giá trị

Nếu như bạn cần phải đo để tính bán kính thì đầu tiên ta cần kiếm một sợi dây đủ dài để có thể quấn quanh được hình cầu đó. Tiếp theo thì ta tiến hành dùng đoạn dây này để quấn quanh hình cầu tại phần rộng nhất rồi đánh dấu giao điểm của đoạn dây đó. Sau đó dùng thước kẻ để đo đoạn dây đó thì ta sẽ có được giá trị chu vi, chia giá trị đó cho 2π hoặc là 6.28 để tính bán kính của hình cầu.

• Hình lăng trụ

Hình trụ là khối không gian có hai đáy phẳng là hai hình tròn có kích thước bằng nhau và một mặt cong được nối liền với hai đáy.

– Công thức tính thể tích của hình lăng trụ

Ta có công thức như sau: V = πr²h

=> Trong đó:

• V là thể tích
• r là bán kính mặt đáy
• h là chiều cao
• π là hằng số có giá trị là 3.14

Đối với hình trụ tròn thì diện tích mặt đáy sẽ được tính hình tròn bán kính r là πr².

– Cách tìm bán kính mặt đáy

Nếu như giá trị của đường kính mặt đáy thì bạn chỉ cần chia giá trị đó cho 2 sẽ được bán kính.

– Tiến hành đo hình trụ để tính bán kính của mặt đáy

Đầu tiên bạn cần phải tìm và đo phần rộng nhất của mặt đáy và chia giá trị đó cho 2 để có được giá trị bán kính. Hoặc bạn có thể đo chu vi của mặt đáy bằng thước dây sau đó đo lại bằng thước kẻ. Có được chu vi thì ta áp dụng luôn cho công thức: C (chu vi) = 2πr. Chia chu vi đó cho 2π hoặc là 6.28 thì bạn sẽ tính được bán kính.

• Hình chóp

Hình chóp là khối không gian có đáy là một đa giác và có các mặt bên giao nhau tại một điểm chính là đỉnh của hình chóp. Hình chóp đa giác đều là hình chóp có tất cả các cạnh bằng đa giác bằng nhau và có tất cả các góc của đa giác cũng bằng nhau.

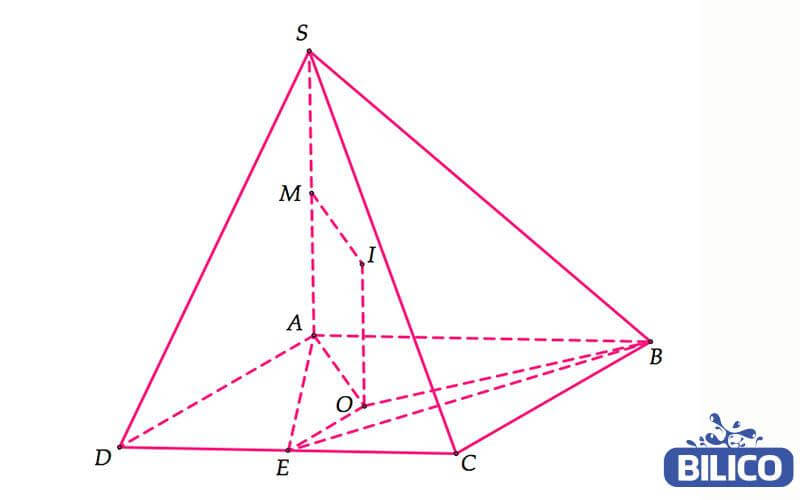
Hình chóp với đáy là hình vuông và có các mặt của hình chóp sẽ giao nhau tại một điểm nhưng các mặt đáy có thể có 5,6 hoặc lên đến 100 cạnh.

– Công thức tính thể tích của hình chóp

Công thức được tính như sau: V=1/3bh

=> Trong đó:

• b là thể tích mặt đáy
• h là chiều cao hình chóp đồng thời cũng là khoảng cách từ đỉnh của hình chóp đến đáy.

– Cách tính diện tích của mặt đáy

Công thức tính diện tích của mặt đáy sẽ phải phụ thuộc vào số cạnh của đa giác. Đối với hình chóp trong giản đồ mặt đáy là hình vuông với các cạnh có kích thước sẽ là 6 inches thì ta sẽ có công thức như sau: A = s2, s sẽ là chiều dài cạnh hình vuông. Vậy đối với hình chóp này thì diện tích của mặt đáy sẽ là 36 in 2.

– Công thức tính thể tích hình chóp có đáy là tam giác

A = 1/2bh

=> Trong đó:

• b là diện tích của đáy
• h chính là chiều cao.

Ta cũng có thể tính diện tích của bất cứ đa giác nào bằng công thức là A = 1/2pa. Trong đó thì a là diện tích, p là chu vi và a chính là trung đoạn là khoảng cách từ tâm của đa giác đến trung điểm của cạnh bất kỳ.

Ứng dụng trong thực tế

Các công thức tính thể tích trên được áp dụng vào thực tế như sau:

1. Ứng dụng để tính thể tích bể bơi.
2. Ứng dụng để tính thể tích nước đóng chai.
3. Ứng dụng để tính thể tích xăng
4. Ứng dụng để tính thể tích dầu.
5. Ứng dụng để tính thể tích cát.
6. Ứng dụng để tính thể tích vật liệu xây dựng như là xi măng,…

Trên đây là các công thức tính thể tích mà Bilico đã tổng hợp các bạn có thể tham khảo. Các công thức này được ứng dụng rất phổ biến trong thực tế. Hãy theo dõi chúng tôi để có thêm nhiều thông tin bổ ích nhé!